QUANDO A TRIONFARE È
LA TRADIZIONE E NON L’INNOVAZIONE

Che cosa accomuna i mutui alla francese con la questione del crollo del viadotto Morandi, i ponti romani con le montagne russe, la pista del salto con gli sci con il Golden Gate Bridge? Oltre a questi, ci sono tanti altri casi in reciproca e intima correlazione, poco evidente, ma che sono ricamati l’uno con l’altro. Siamo circondati da una connessione profonda tra fatti diversi, uniti da una sola formula sottostante, di fronte alla quale, la maggior parte di noi è indifferente.

Partiamo dai ponti romani, che furono progettati e realizzati da architetti che non conoscevano le derivate, né gli integrali e che, per dirla tutta, non avevano neanche lo zero, importato in Europa solo molto più tardi, dagli arabi. I costruttori romani conoscevano solo i numeri naturali; le figure geometriche di cui si servivano erano quelle semplici come il cerchio. Eppure diedero alla luce opere di rara bellezza e armonia, che – come il Colosseo a Roma e l’Arena a Verona – stanno ancora in piedi e rappresentano fari di bellezza per il mondo intero. Sono oltre 900 i ponti romani che in Europa, in Africa del Nord e in Medio Oriente, sono ancora utilizzati: hanno resistito per quasi duemila anni a ogni genere di sfida, naturale o antropica (il ponte di Chaves in Portogallo, ad esempio).

Il Pont du Gard dell’acquedotto in Francia, fu edificato nel 19 avanti Cristo e la città di Roma fu rifornita da ben undici acquedotti, costruiti in pietra calcarea, che avevano una portata di oltre un milione di metri cubi d’acqua giornalieri, sufficienti per 3.5 milioni di persone (varrebbe anche in tempi moderni).

Come fecero i Romani a pensare e rendere concreti modelli simili? Grazie alla loro naturale predisposizione, essi seppero anche accogliere e assimilare le idee altrui; importarono dall’Oriente, con cui erano in stretto contatto, il senso della gravità e della verticalità, la circonferenza e gli archi: su questi concetti basilari elaborarono modelli costruttivi organizzati sui numeri 1, 3, 5, 10, 12 e 60. Quest’ultimo, in particolare fu mutuato dalla cultura sessagesimale babilonese (la circonferenza ha 360 gradi, che è un multiplo di 60, pari a sei volte 10). La costruzione dei ponti nell’antica Roma è stata fatta con ricette semplici, costituite da pochi elementi, espansi lungo tutte le strutture edificate, secondo rapporti di armonia che erano stati introdotti attraverso le scuole pitagoriche della Magna Grecia.

La chiave di tutto – e ciò che unisce tutti questi casi ed esempi, tra loro solo apparentemente disparati – è la cicloide, una curva che si ottiene da un punto su una circonferenza che rotola lungo una retta: i ponti romani stanno in piedi, non solo per la qualità dei prodotti utilizzati e per l’affidabilità del loro assemblaggio, ma anche perché rispettano forme che a loro volta sono intrinsecamente legate a fattori e a processi naturali.

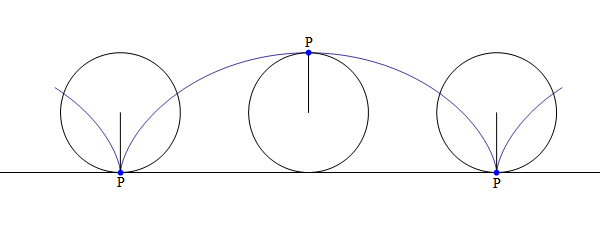La curva cicloide

Un esempio di curva cicloide – in questo caso rovesciata – è costituito dal Golden Gate Bridge, che esiste – e resiste – dal 1937 con i suoi 2,7 chilometri di lunghezza.

Il Golden Gate Bridge

Ora si prenda una curva cicloide classica come quella a base di un ponte romano, la si capovolga come nel ponte di San Francisco, e poi la si inclini: si ottiene una traiettoria dove è possibile scendere da un punto all’altro con la massima velocità. Questa curva è definita brachistocrona (che impiega il tempo più breve per scendere da un punto verso l’altro). Infatti, se si immagina di lasciar cadere o scivolare una palla lungo la diagonale di un quadrato (tipicamente un piano inclinato), dove tra i due punti iniziale e finale è poi inserita anche una curva brachistocrona, si noterà che il tragitto di discesa è compiuto in un tempo inferiore lungo la curva, perché in diagonale, sul piano inclinato, il periodo di tempo che impiega la palla che rotola nel suo percorso è più lungo.

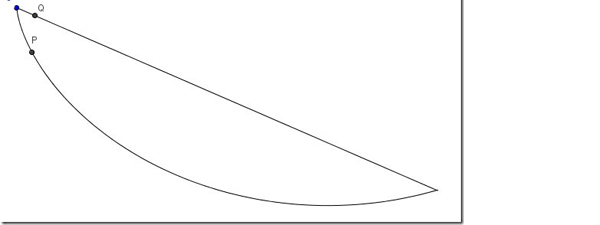
La curva cicloide rovesciata (brachistocrona) e il piano inclinato

Per la discesa di un corpo la curva brachistocrona è più veloce della diagonale dritta del piano inclinato. E’ su questo modello, di cicloidi e brachistocrone che sono costruite le montagne russe. I trampolini per il salto con gli sci sono delle brachistocrone pure: esse consentono una forte accelerazione nella fase iniziale, che permette di accumulare energia cinetica, la quale a sua volta fornisce l’intensità della spinta per il salto finale. Lo stesso criterio è riscontrabile nelle piste da skateboard, dove si correlano tempo, spazio e velocità secondo precise proporzioni.

Dal punto di vista della formula matematica che lo presiede, anche il mutuo alla francese è rappresentabile come una curva cicloide brachistocrona: seguendo il flusso del denaro come fosse una sfera, all’inizio le quote di interesse sono molto alte e decrescono decelerando lungo la curva, con una forza analoga all’accelerazione delle quote di capitale da corrispondere.

Il mutuo alla francese

Resta da vedere e valutare infine il ponte Morandi, che non è stato progettato su una cicloide: è stato costruito con modelli differenziali e integrali, senza alcun riferimento alla circolarità, (che invece ammette in sé il rispetto del tempo, della gravità della terra e anche dell’accelerazione naturale dei corpi). La sua struttura prevedeva campate con cavalletti e stralli su geometrie triangolari. Un’idea artificiale, pura divagazione formale per testimoniare quanto l’idea possa avere in sé forze in grado di vincere la natura. Forse anche per questo il viadotto di Genova è crollato, per il suo essere contro l’armonia circolare dei cicli della natura. Un esempio tragico di come un salto innovativo non significhi necessariamente essere meglio della tradizione, cancellata con un gesto presuntuoso.

Continua a leggere

Condividi